The Significance of Distance Measures in AI and ML Algorithms

Let’s delve deeper into each of these distance measures to provide a more thorough understanding:

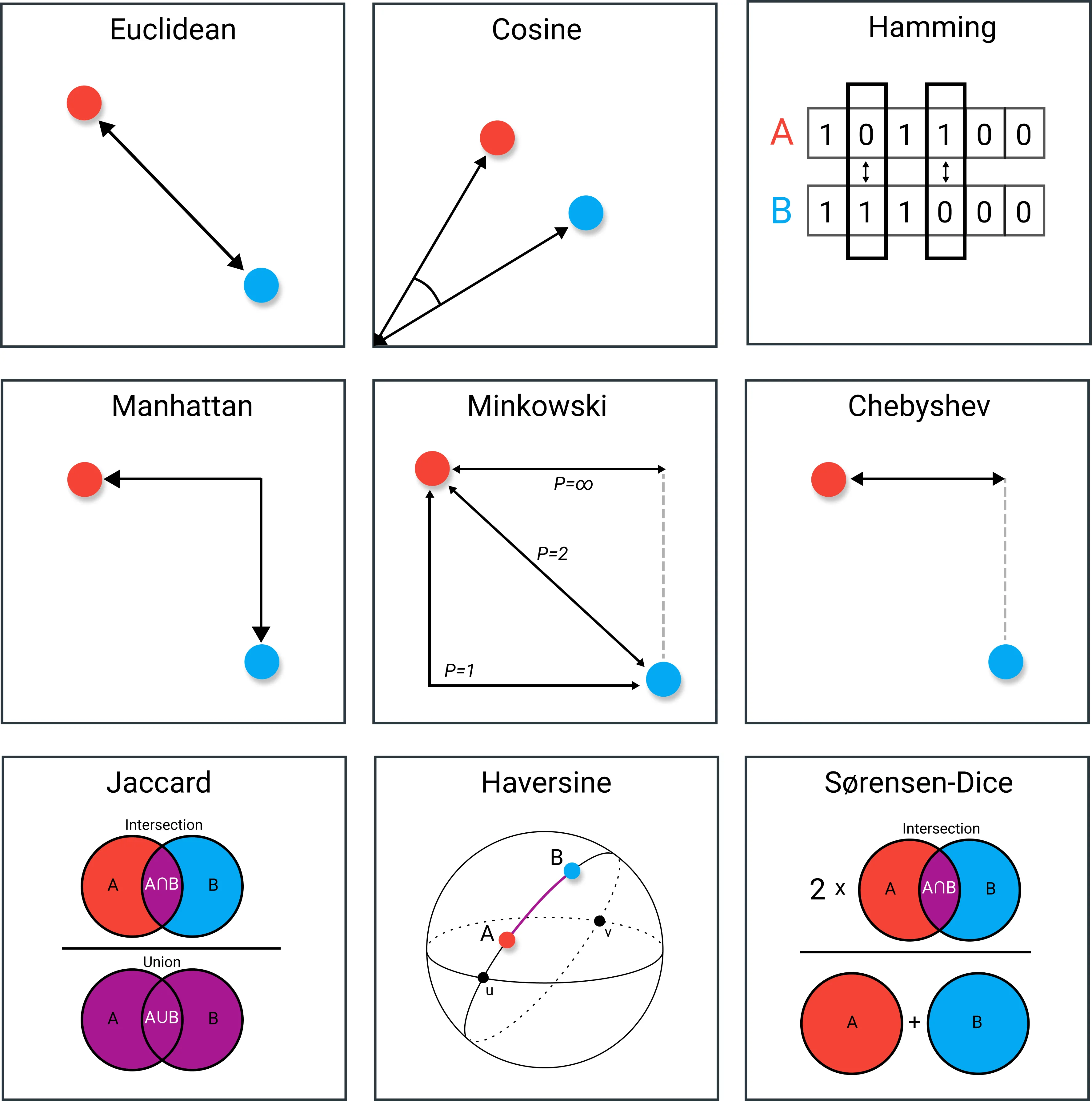
1. Euclidean Distance:
   • This distance metric is derived from the Pythagorean theorem and represents the shortest straight-line distance between two points in a space with multiple dimensions.
   • In addition to its applications in machine learning algorithms like KNN and K-Means, Euclidean Distance is fundamental in fields such as physics, engineering, and computer graphics.
   • Understanding Euclidean Distance helps in visualizing geometric concepts and spatial relationships in higher dimensions.
2. Cosine Similarity:
   • Unlike Euclidean Distance, which considers both magnitude and direction, Cosine Similarity solely focuses on the direction of vectors, making it particularly suited for tasks where the magnitude of the vectors is less relevant.
   • It’s widely used in natural language processing (NLP) tasks such as document similarity, text classification, and recommendation systems.
   • Cosine Similarity measures the cosine of the angle between two vectors, ranging from -1 (completely opposite) to 1 (completely aligned), providing a measure of similarity between documents or features.
3. Hamming Distance:
   • This metric is primarily utilized in digital communication and error correction codes.
   • It calculates the number of differing bits between two binary strings of equal length, making it effective in detecting and correcting errors in transmitted data.
   • Understanding Hamming Distance is crucial in ensuring data integrity and reliability in digital communication systems.
4. Manhattan Distance:
   • Named after the grid-like layout of Manhattan streets, this distance metric measures the sum of absolute differences between corresponding coordinates of two points.
   • Its applications extend beyond spatial distance measurement to diverse fields such as computer vision, transportation planning, and logistics.
   • Manhattan Distance is particularly useful in scenarios where movement is constrained to grid-like paths, such as in urban environments or when analyzing data with categorical features.
5. Minkowski Distance:
   • This distance metric generalizes both Euclidean and Manhattan distances by introducing a parameter, often denoted as “p,” which determines the degree of similarity.
   • When p=2, Minkowski Distance reduces to Euclidean Distance, while p=1 yields Manhattan Distance.
   • Its versatility makes it suitable for handling datasets with varying relevance of dimensions, a common scenario in machine learning and data analysis.
6. Chebyshev Distance:
   • Named after Pafnuty Chebyshev, this distance metric computes the maximum absolute difference along any dimension between two points in space.
   • It’s often used in games, robotics, and pattern recognition for defining movement costs or evaluating spatial relationships.
   • Chebyshev Distance is particularly handy in scenarios where diagonal movement is allowed or when analyzing data with irregular shapes.
7. Jaccard Index:
   • This similarity coefficient calculates the intersection over union of two sets, providing a measure of overlap between them.
   • It’s extensively employed in information retrieval, clustering, and recommendation systems.
   • Understanding the Jaccard Index helps in quantifying the similarity between sets with categorical data, such as user preferences or item characteristics.
8. Haversine Distance:
   • Named after the Haversine formula, this distance metric computes the shortest distance between two points on the surface of a sphere, considering the curvature of the Earth.
   • It’s essential in navigation, geolocation services, and geographic information systems (GIS).
   • Haversine Distance facilitates accurate distance calculations for applications ranging from route planning to tracking wildlife migration patterns.
9. Sorensen-Dice Coefficient:
   • This coefficient measures the similarity between two samples based on the size of their shared elements.
   • It’s commonly used in fields such as biology (for comparing genetic sequences), information retrieval (for document similarity), and image processing (for object recognition).
   • Understanding the Sorensen-Dice Coefficient aids in assessing the degree of overlap or agreement between samples, guiding decision-making in various analytical tasks.

Reference

• 9 Distance Measures in Data Science